前言

今天將會用Sarsa與Q Learning，來挑戰Taxi環境。之前Monte Carlo Methood在taxi環境上會有收斂過久的問題，這是因為Monte Carlo需要等到整個episode結束後才會更新。但如果使用TD Learning，將能在一定的時間內收斂。

Taxi

我們一樣先匯入需要的函式與變數

import gym
import numpy as np
import sys
from collections import defaultdict

env = gym.make('Taxi-v2')

num_episodes = 500000
gamma = 1.0
epsilon = 0.1
alpha = 0.1

跟之前不同的是，多了alpha與total_reward，alpha就是昨天提到的learning rate

Sarsa

從算法中可發現，我們Value Function的更新需要兩個action，時間點的Action與時間點的Action。依算法實作即可。

def choose_action(state, Q):
    if np.random.rand() < epsilon:
        return np.random.randint(env.action_space.n)
    else:
        return np.argmax(Q[state])

def sarsa_update_value(state, action, reward, next_state, next_action, done, Q):
    if done:
        Q[state][action] += alpha * (reward - Q[state][action])
    else:
        Q[state][action] += alpha * (reward + gamma * Q[next_state][next_action] - Q[state][action])

def run_sarsa(num_episodes, render = False):
    Q = defaultdict(lambda: np.zeros(env.action_space.n))
    total_reward = []
    for i in range(num_episodes):
        rewards = 0
        state = env.reset()
        action = choose_action(state, Q)
        while True:
            if i == num_episodes - 1 and render:
                env.render()
            next_state, reward, done, info = env.step(action)
            next_action = choose_action(next_state, Q)
            sarsa_update_value(state, action, reward, next_state, next_action, done, Q)
            rewards += reward
            if done:
                break
            state, action = next_state, next_action
        total_reward.append(rewards)
        print(f'\repisode: {i + 1}/{num_episodes}', end = '')
        sys.stdout.flush()
    print(f'\nMax Reward: {max(total_reward)}')
    return total_reward
   
run_sarsa(num_episodes, True)

• choose_action()是以-greedy來決定policy，事實上也可以用其他機率分布來取代。
• sarsa_update_value()就是算法中的更新公式
• total_reward用來記錄每個episode中得到的reward
• 這邊Q與Monte Carlo中的Q一樣使用defaultdict，可以應付state數量不明確的情況

Expected Sarsa

Expected Sarsa與Sarsa不同的是，更新不再需要下個時間點的Action，而是改為以期望值來更新。要注意的是這邊期望值是依照-greedy的機率來決定。

def expected_sarsa_update_value(state, action, reward, next_state, done, Q):
    if done:
        Q[state][action] += alpha * (reward - Q[state][action])
    else:
        policy = np.ones(env.action_space.n) * epsilon / env.action_space.n
        policy[np.argmax(Q[next_state])] += 1 - epsilon
        Q[state][action] += alpha * (reward + gamma * np.dot(policy, Q[next_state]) - Q[state][action])
def run_expected_sarsa(num_episodes, render = False):
    Q = defaultdict(lambda: np.zeros(env.action_space.n))
    total_reward = []
    for i in range(num_episodes):
        rewards = 0
        state = env.reset()
        while True:
            if i == num_episodes - 1 and render:
                env.render()
            action = choose_action(state, Q)
            next_state, reward, done, info = env.step(action, Q)
            expected_sarsa_update_value(state, action, reward, next_state, done, Q)
            rewards += reward
            if done:
                break
            state = next_state
        total_reward.append(rewards)
        print(f'\repisode: {i + 1}/{num_episodes}', end = '')
        sys.stdout.flush()
    print(f'\nMax Reward: {max(total_reward)}')
    return total_reward
    
run_expected_sarsa(num_episodes, True)

• 將Sarsa的更新方法改為期望值的更新
• 與環境互動不再需要提前一個state做action

Q Learning

Q Learning與Expected Sarsa一樣只需要當前的Action來更新，更新的策略是以optimal value function的方向來更新。

def q_update_value(state, action, reward, next_state, done, Q):
    if done:
        Q[state][action] += alpha * (reward - Q[state][action])
    else:
        Q[state][action] += alpha * (reward + gamma * np.max(Q[next_state]) - Q[state][action])
def run_q_learning(num_episodes, render = False):
    Q = defaultdict(lambda: np.zeros(env.action_space.n))
    total_reward = []
    for i in range(num_episodes):
        rewards = 0
        state = env.reset()
        while True:
            if i == num_episodes - 1 and render:
                env.render()
            action = choose_action(state, Q)
            next_state, reward, done, info = env.step(action)
            q_update_value(state, action, reward, next_state, done, Q)
            rewards += reward
            if done:
                break
            state = next_state
        total_reward.append(rewards)
        print(f'\repisode: {i + 1}/{num_episodes}', end = '')
        sys.stdout.flush()
    print(f'\nMax Reward: {max(total_reward)}')
    return total_reward
    
run_q_learning(num_episodes, True)

• 環境互動方式與expected sarsa一樣
• q_update_value()是以max的方式更新

Evaluation

我們可以實際將total_reward的趨勢圖畫出來，看看三種算法的差別。
將每個算法跑100次後得到的total_reward平均，每次皆跑1000個episode

import matplotlib.pyplot as plt
sarsa_reward = [0 for i in range(500)]
expected_sarsa_reward = [0 for i in range(500)]
q_reward = [0 for i in range(500)]
for i in range(100):
    sarsa_reward = [sum(x) for x in zip(sarsa_reward, run_sarsa(1000))]
    expected_sarsa_reward = [sum(x) for x in zip(expected_sarsa_reward, run_expected_sarsa(1000))]
    q_reward = [sum(x) for x in zip(q_reward, run_q_learning(1000))]
    
sarsa_reward = np.array(sarsa_reward) / 100
expected_sarsa_reward = np.array(expected_sarsa_reward) / 100
q_reward = np.array(q_reward) / 100
plt.plot(sarsa_reward)
plt.plot(expected_sarsa_reward)
plt.plot(q_reward)
plt.legend(['sarss reward', 'expected sarsa reward', 'q learning reward'])
plt.show()

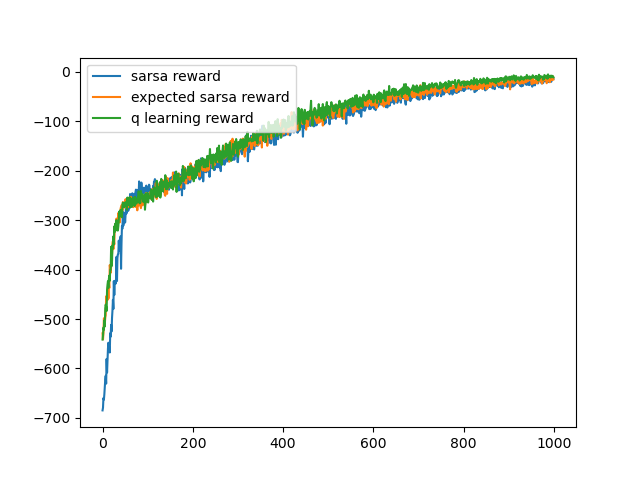
可以看到sarsa初期得到的reward較少，而差不多在50個episode後，三者的收斂速度是一樣的。

總結

明天將會介紹Sarsa與Q Learning間的差異，以及更進階的n-step TD Learning。